| Dernières réponses | |  Héritage Héritage
Des frères se partagent un héritage.
Le premier prend 1000 € et 10% du reste,
le deuxième prend 2000 € et 10% du reste,
le troisième prend 3000€ et 10% du reste et ainsi de suite.
A la fin ils ont exactement la même part.
Combien y a-t-il de frères? A combien se monte l'héritage?
De Kalmina
de passage sur le forum :
tous les enfants ont la même part.
soit X l"héritage .
1) le premier touche 1000 + 10% (X-1000)
=> reste donc dans la cagnotte Y = X - 1000 - 10% (X-1000) = 90% X - 900
2) Le deuxième touche 2000 + 10 % (Y - 2000)
Les somme sont les mêmes
900 + 10% X = 1800 + 10% ( 90%X - 900)
10% X = 900 + 9%X - 90
1%X = 810
X = 81.000 euros.
le premier recoit 9000 => reste 72000
Le deuxième recoit 9000 => reste 63000 ....
etc il y a 9 frères
De Kalmina |
| |  Archimède Archimède
Une grosse ancre dans un petit bateau qui flotte sur un petit lac fermé.L'ancre tombe à l'eau et coule.Que devient le niveau du lac ?
De Kalmina
logiquement le niveau de l'eau baisse !
explication : Avant l'ancre flottait (car elle était sur le bateau) donc elle equivalait à son poids en volume d'eau dans le lac. (pas très clair mon truc là ? euh dit autrement quand on a chargé l'ancre sur le bateau , le niveau du lac à monter autant que si on avait rajouté X litres d'eau dans le lac avec X le poids de l'ancre)
Après l'ancre cool et touche le fond! donc le niveau d'eau ne varie plus en fonction du poids mais du volume de l'ancre..
De Kalmina
|
| |  Serrez moi la pince, Monseigneur ! Serrez moi la pince, Monseigneur !
A la fin d'une soirée protocolaire où étaient reçus exclusivement des couples, 312 poignées de mains ont été échangées, chaque convive saluant tous les autres sauf son conjoint. Combien y avait-il de couples ?
De Kalmina
13 couples
De Loupnoir
13 couples => 2*24 poignées de mains par couple 48 *13 / 2 (division par 2 car là j'ai compté les poignées de mains vues de chaque participant )
24*13 = 312
|
| |  Quatre poids, quarante mesures Quatre poids, quarante mesures
Papi Germain, ayant un commerce de vente en vrac, a besoin d'une unité de mesure efficace lui permettant de peser ses ventes, qui se font uniquement par tranche de un kilo.
Mais comme il n'a qu'une balance à plateaux, il lui faut des poids étalonnés.
Il achète donc une barre de 40 kg, qui coupée en 4 morceaux seulement, lui permettra de peser 0toutes ses ventes de 1 à 40 kg.
Quel est le poids de chacun des morceaux?
De Kalmina
Soit 1-3-9-27
De Loupnoir
|
| | 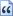 Les pions Les pions
Comment placer quatre pions dans cette grille, de manière qu'aucun pion ne se trouve sur la même ligne, colonne ou diagonale ?
(c'est un carré de 4 colonnes par 4 lignes)
De Kalmina
X O XX
XXX O
O XXX
XX O X
De Loupnoir
|
| |  Le partage des chameaux Le partage des chameaux
Un vieil homme, à l'approche de sa mort, décide de partager son troupeau de 17 chameaux entre ses trois fils. L'aîné héritera de la moitié du troupeau, le cadet du tiers et le benjamin du neuvième. Confrontés à l'indivisibilité de 17 par 2, 3 et 9, les trois frères vont trouver le sage du village. Celui-ci, fin mathématicien, leur propose une solution qui, sans avoir recours à une boucherie, respecte les volontés du vieil homme. Comment a-t-il fait ?
De Kalmina
Les chameaux ne pouvant être coupés il donne 9 chameaux à l'ainé, 6 au cadet et 2 au benjamin ce qui fait approximativement les 1/2, 1/3 et 1/9 et 17 chameaux.Soit en rajoutant un chameau pour avoir 18 chameaux et il récupère à la fin le chameau qu'il a rajouté..
De loupnoir et Kalmina
|
| |  Boire un p'tit coup ! Boire un p'tit coup !
Si l'on fixe le prix d'une bouteille de beaujolais à 20 F, sachant que le vin coûte 19 F de plus que la bouteille, combien vaut la bouteille ?
De Kalmina
Je dirais 0,5 centimes pour le vin.
de loupnoir
|
| |  Les jumeaux Les jumeaux
Nous sommes nés de la même mère, le même jour et à la même heure, le même mois et la même année.Pourtant nous ne sommes pas jumeaux.Pourquoi ?
De Kalmina
Car se sont des filles donc des jumelles
De loupnoir
|
| |  Les sacs de pièces Les sacs de pièces
Vous avez 10 tas de pièces : 9 tas de vraies pièces et 1 tas de fausses pièces.
Vous avez à votre disposition une balance numérique, capable de vous indiquer le poids au gramme près.
Sachant qu’une vraie pièce pèse 100 grammes, et qu’une fausse en pèse 110, déterminer quel est le tas de fausses en pièces en effectuant qu’une seule et unique pesée .
De Kalmina
Je numérote les sacs ou je les aligne pour les reconnaitre.
dans le premier sac je prend 1 pièce
dans le second sac, 2 pièces
dans le troisième sac, 3 pièces
...
dans le dixième sac, 10 pièces
J'ai donc pris : 1 + 2 + 3 +... + 10 = 55 pièces
si toutes ces pièces étaient vraies j'aurais : 55 x 100 g = 5,5 kg
mais dans le sac n° N j'ai des fausses pièces qui pèsent 10 g de plus et dans ce sac j'ai justement pris N pièces.
J'ai donc N x 10 g en plus des 5,5 kg.
si j'ai 10g de plus les fausses pièces sont dans le 1er sac
si j'ai 20g de plus, elles sont dans le 2ème sac
si j'ai 30g de plus, elles sont dans le 3ème sac
etc....
si j'ai 100g de plus, elles sont dans le 10ème sac
D'où poids total des pièces 55 x 100g + N x 10g où N est le n° (ou le rang) du sac de fausses pièces.
de Minnie |
| |  Les trois prisonniers Les trois prisonniers
Trois prisonniers sont condamnés. On propose d'accorder à au moins l'un d'entre eux de s'en sortir.
On place une marque dans le dos des prisonniers. S'ils ont le dos marqué et s'il arrivent à deviner qu'ils ont une marque, alors ils peuvent sortir.
Bien sûr, les prisonniers ne peuvent communiquer entre eux, ils peuvent juste contempler le dos de leurs collègues et réfléchir.
Chaque prisonnier voit que le dos de ses deux camarades est marqué, mais ne peut pas voir ce qu'il y a dans son propre dos. Comment font-ils pour sortir tout les trois ?
De Kalmina
Au moins un prisionnier est marqué donc si un des 2 prisonniers voyait que ses 2 compatriote n'ont pas de marque, il sortirait immédiatement (ca voudrait dire qu'il est marqué lui).
Mais comme aucun prisonnier ne sort de suite, ils observent le comportement des autres prisionnier.
Il apparaît alors clairement que tous les prisionniers voit minimum une marque et que donc au moins 2 prisonniers sont marqués. Chaque prisonnier peut arriver a ce stade de la réflexion.
Donc si 2 prisonniers sont marqué, seul hésiterons encore les prisionners qui voit 2 marques. Comme tous hesitent, il voit donc tous 2 marques . Tout le monde est marqué. donc tout le monde sort.
De Kalmina
|
|
|